coolliyong.github.io

树

树的定义

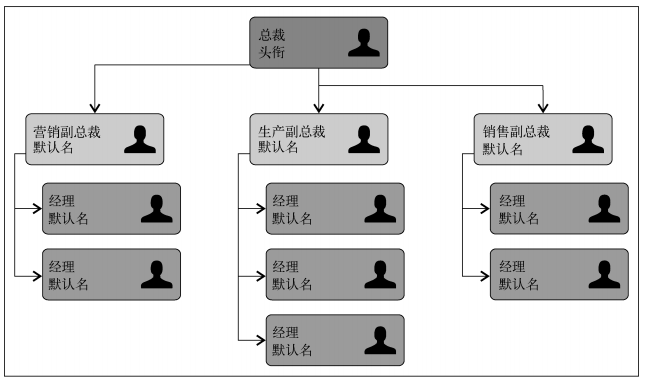
树是一种分层数据的抽象模型。现实生活中最常见的树的例子是家谱，或是公司的组织架构图,如下图所示：

树的相关术语

一个树结构包含一系列存在父子关系的节点。每个节点都有一个父节点（除了顶部的第一个节点）以及零个或多个子节点

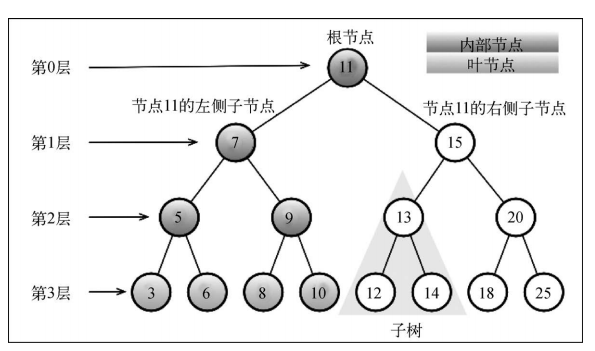
• 结点的度：结点拥有的子树的数目。eg：结点 A 的度为 3
• 树的度：树种各结点度的最大值。eg：树的度为 3
• 叶子结点：度为 0 的结点。g：E、F、C、G 为叶子结点
• 孩子结点：一个结点的子树的根节点。eg：B、C、D 为 A 的子结点
• 双亲结点：B 为 A 的子结点，那么 A 为 B 的双亲结点
• 兄弟结点：一个双亲结点结点的孩子互为兄弟结点。eg：B、C、D 为兄弟结点
• 结点的层次：根节点为第一层，子结点为第二层，依次向下递推…eg：E、F、G 的层次均为 3
• 树的深度：树种结点的最大深度。eg：该树的深度为 3
• 森林：m 棵互不相交的树称为森林

二叉搜索树搜索和新增

// 生成构造类
function BinarySearchTree() {
  // 静态类，生成节点
  BinarySearchTree.createNode = function(key) {
    this.key = key
    this.left = null
    this.right = null
  }

  this.root = null
}

// 二叉树插入
BinarySearchTree.prototype.insert = function(key) {
  const node = new BinarySearchTree.createNode(key)

  if (!this.root) {
    this.root = node
    return true
  }

  let cur = this.root
  while (cur) {
    // 小于 = left
    if (key < cur.key) {
      if (cur.left) {
        cur = cur.left
      } else {
        cur.left = node
        return true
      }
    } else {
      if (cur.right) {
        cur = cur.right
      } else {
        cur.right = node
        return true
      }
    }
  }
}

// 二叉树搜索
BinarySearchTree.prototype.search = function(key) {
  let cur = this.root
  while (cur) {
    if (key === cur.key) {
      return true
    }
    // 小于 = left
    if (key < cur.key) {
      cur = cur.left
    } else {
      cur = cur.right
    }
  }
  return false
}

const bst = new BinarySearchTree()

bst.insert(47)
bst.insert(15)
bst.insert(78)
bst.insert(82)
bst.insert(57)
bst.insert(87)
bst.insert(76)
bst.insert(65)
bst.insert(94)
bst.insert(80)

console.log(bst.root)

bst.search(15)

二叉搜索树遍历

想到的第一个方式就是先序遍历，然后翻看了一下书，遍历有三种方式，真是让人头大

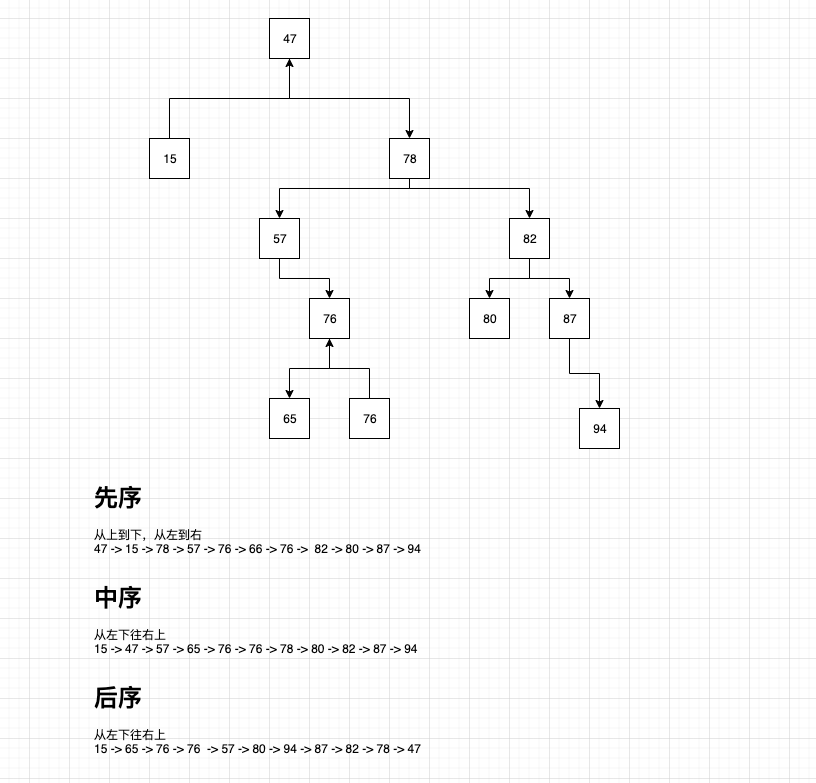
二叉搜索树遍历代码实现

// 这种叫先序遍历
BinarySearchTree.prototype.preOrderTraverseNode = function(callback) {
  // 从上到下 从左到右
  if (this.root) node1(this.root)

  function node1(node) {
    if (node === null) return
    // 从上往下从左往右先输出节点再遍历
    callback && callback(node.key)
    if (node.left) node1(node.left)
    if (node.right) node1(node.right)
  }
}

// 中序遍历
BinarySearchTree.prototype.inOrderTraverse = function(callback) {
  inOrderTraverseNode(this.root, callback)

  function inOrderTraverseNode(node, callback) {
    if (node !== null) {
      inOrderTraverseNode(node.left, callback)
      callback && callback(node.key)
      inOrderTraverseNode(node.right, callback)
    }
  }
}

// 后序遍历
BinarySearchTree.prototype.postOrderTraverse = function(callback) {
  postOrderTraverseNode(this.root, callback)

  function postOrderTraverseNode(node, callback) {
    if (node !== null) {
      //{2}
      postOrderTraverseNode(node.left, callback)
      postOrderTraverseNode(node.right, callback)
      callback && callback(node.key)
    }
  }
}

二叉搜索树最大值和最小值

BinarySearchTree.prototype.min = function() {
  let cur = this.root
  if (!cur) return null
  while (cur.left) {
    cur = cur.left
  }
  return cur.key
}

BinarySearchTree.prototype.max = function() {
  let cur = this.root
  if (!cur) return null
  while (cur.right) {
    cur = cur.right
  }
  return cur.key
}

二叉搜索树删除节点

删除略复杂，需要考虑以下三种情况

1. 删除叶子节点
2. 删除只有左/右一个子节点的的节点
3. 删除子树（有左右两颗子树的节点）

首先需要分析：如果删除了节点，那需要找一个元素来替代

假设删除的节点是15，此时需要 15的 右边20 下找出最小的节点 -> 18 把18提取到15的位置，此时左边的的节点依旧是小于18，右边大于18

假设删除的节点是12，此时直接把 13.left = null 现在假设树种已经没有12这个节点，这时如果再删除13，直接把14这个节点提上去替换13

BinarySearchTree.prototype.remove = function (key) {
  if (!this.root) return null

  let cur = this.root,
    prev = null,
    flag = 'left'

  while (cur.key !== key) {
    prev = cur
    if (cur.key < key) {
      cur = cur.right
      flag = 'right'
    } else {
      flag = 'left'
      cur = cur.left
    }
    // 如果往下查找已经是null了 pass
    if (cur === null) return null
  }

  // 如果删除的是一颗缺少左右节点的树
  if (cur.left === null) {
    prev[flag] = cur.right;
    return cur
  } else if (cur.right === null) {
    prev[flag] = cur.left;
    return cur
  }

  // 删除的是一个叶子节点，没有左右节点
  if (cur.left === null && cur.right === null) {
    prev[flag] = null
    return cur
  }

  // 如果删除的是一颗子树，则从右儿子里取出最小的一个
  // 删除当前子树的顶点，然后把找出的节点替换到当前
  if (cur.left !== left && cur.right !== null) {
    //  如果左右节点都不为空
    let _cur = cur.right,
      _prev = cur
    while (_cur.left) {
      _prev = _cur
      _cur = _cur.left
    }
    // 找到最下面的左子树之后需要处理原来左子树的数据 它只可能有右子树的节点，不可能有左子树的节点
    _prev.left = _cur.right

    // 原来左子树
    _cur.left = cur.left
    // 原来右子树
    _cur.right = cur.right
    // 替换原来节点
    prev[flag] = _cur
    return _cur

  }
}